In water-drive reservoirs, the relation between Gp and p/z is not linear, as can be seen by an inspection of Eqs. (4.13) and (4.16). Because of the water influx, the pressure drops less rapidly with production than under volumetric control, as shown in the upper curve of Fig. 4.2. Consequently, the extrapolation technique described for volumetric reservoirs is not applicable. Also, where there is water influx, the initial gas in place calculated at successive stages of depletion, assuming no water influx, takes on successively higher values, whereas with volumetric reservoirs the calculated values of the initial gas should remain substantially constant.Equation (4.13) may be expressed in terms of the initial pore volume, Vi, by recognizing that Vi= GBgi and using Eq. (2.15) for Bg and Bgi:
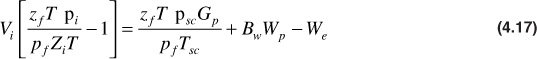
For volumetric reservoirs, discussed in the previous section, this equation can be reduced and rearranged to give

Examples 4.2, 4.3, and 4.4 illustrate the use of the various equations that we have described in gas reservoir calculations.
Example 4.2 Calculating the Initial Gas in Place and the Initial Reserve of a Gas Reservoir from Pressure-Production Data for a Volumetric Reservoir
Given
Base pressure = 15.025 psia
Initial pressure = 3250 psia
Reservoir temperature = 213°F
Standard pressure = 15.025 psia
Standard temperature = 60°F
Cumulative production = 1.00 × 109 SCF
Average reservoir pressure = 2864 psia
Gas deviation factor at 3250 psia = 0.910
Gas deviation factor at 2864 psia = 0.888
Gas deviation factor at 500 psia = 0.951
Solution
Solve Eq. (4.18) for the reservoir gas pore volume Vi:
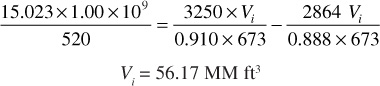
The initial gas in place by the real gas law is
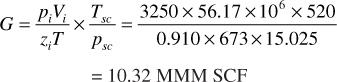
The gas remaining at 500-psia abandonment pressure is
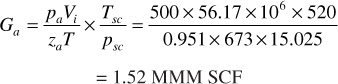
The initial gas reserve based on a 500-psia abandonment pressure is the difference between the initial gas in place and the gas remaining at 500 psia, or
Gr = G – Ga = (10.32 – 1.52) × 109
= 8.80 MMM SCF
Leave a Reply