In the previous sections, the initial gas in place was calculated on a unit basis of 1 ac-ft of bulk productive rock, given information on the porosity and connate water. To calculate the initial gas in place on any particular portion of a reservoir, it is necessary to know, in addition, the bulk volume of that portion of the reservoir. If the porosity, connate water, and/or bulk volumes are not known with any reasonable precision, the methods described cannot be used. In this case, the material balance method may be used to calculate the initial gas in place; however, this method is applicable only to the reservoir as a whole because of the migration of gas from one portion of the reservoir to another in both volumetric and water-drive reservoirs.
The general material balance equation for a gas reservoir is derived in Chapter 3:
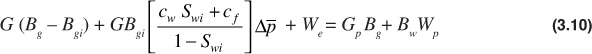
Equation (3.10) could have been derived by applying the law of conservation of mass to the reservoir and associated production.For most gas reservoirs, the gas compressibility term is much greater than the formation and water compressibilities, and the second term on the left-hand side of Eq. (3.10) becomes negligible:

When reservoir pressures are abnormally high, this term is not negligible and should not be ignored. This situation is discussed in a later section of this chapter.
4.3.1 Material Balance in Volumetric Gas Reservoirs
For a volumetric gas reservoir, Eq. (4.13) can be reduced to a simple application of a straight line involving the gas produced, its composition, and the reservoir pressure. This relationship is routinely used by reservoir engineers to predict recoveries from volumetric reservoirs. Since there is neither water encroachment norwater production in this type of a reservoir, Eq. (4.13) reduces to

Using Eq. (2.15) and substituting expressions for Bg and Bgi into Eq. (4.14), the following is obtained:

Noting that production is essentially an isothermal process (i.e., the reservoir temperature remains constant), then Eq. (4.15) is reduced to

This can be rearranged as

Because pi, zi, and G are constants for a given reservoir, Eq. (4.16) suggests that aplot of p/z as the ordinate versus Gp as the abscissa would yield a straight line, with

This plot is shown in Fig. 4.2.
If p/z is set equal to zero, which would represent the production of all the gas from a reservoir, then the corresponding Gp equals G, the initial gas in place. The plot could also be extrapolated to any abandonment p/z to find the initial reserve. Usually this extrapolation requires at least 3 years of accurate pressure depletion and gas production data.
Leave a Reply